Efficiency Calculation

There are mainly three types of efficiencies of a positive displacement machine, such as volumetric efficiency, hydromechanical efficiency and total efficiency. The leakages and compressibility losses affect the so-called volumetric performance of the hydraulic machine, which can be quantified by the parameter volumetric efficiency. Volumetric efficiency of a pump is defined as the ratio of effective output flow to the ideal output flow. Mathematically, it can be expressed as:

\[\eta_{v,P} = \frac{Q_{P,e}}{Q_{P,i}}\]

Where \(Q_{P,e}\) represents the effective output flow and \(Q_{P,i}\) represents the derived output flow. Now derived output flow can be calculated using,

\[Q_{P,i} = n_{P} \cdot V_{D,P}\]

Where \(n_{P}\) represents the shaft rotational speed of the pump, \(V_{D,P}\) represents the displacement chamber volume of the pump.

Since for an actual motor the leakages cause a lower rotational shaft speed, with respect to the ideal case, the volumetric efficiency is defined as the ratio between the actual shaft speed and the ideal one.

\[\eta_{v,M} = \frac{n_{M,e}}{n_{M,i}} = \frac{n_{M,e} \cdot V_{D,M}}{Q_{M,e}}\]

Where \(n_{M,e}\) represents the effective shaft rotational speed, \(n_{M,i}\) represents the ideal shaft rotational speed of the motor, \(V_{D,M}\) is the displacement chamber volume of the motor, and \(Q_{M,e}\) represents the effective input flow.

Volumetric efficiency calculation is demonstrated below using a case of an axial piston pump. For an axial piston pump, derived or ideal output flow can be calculated as

\[Q_{P,i} = Z \cdot n \cdot V_{D,P}\]

Where Z represents the number of pistons. Now \(V_{D,P}\) is equal to the piston area \(A_{k}\) times the stroke length \(s_{k}\) Again,

\[A_{k} = \frac{\pi}{4} (d_{k})^2\]

Here \(d_{k}\) represents the piston diameter.

\[s_{k} = 2 \cdot R \cdot \tan(\beta)\]

Here R represents the pitch radius and \(\beta\) represents the swashplate angle.

The effective flow rate provided by the pump can be found using the simulation results. outletChamber net volume flow provides the instantaneous effective output flow rates \(Q_{P,e}\) for different time steps.

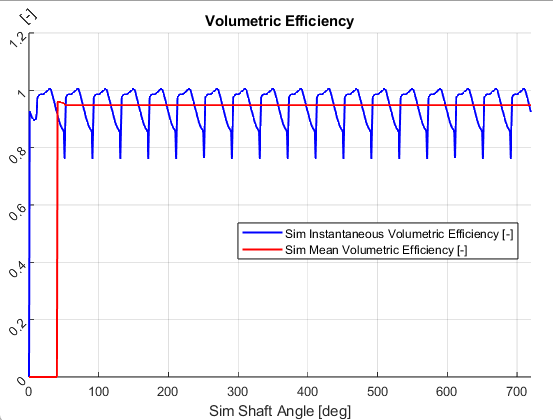
The mean volumetric efficiency is calculated considering the moving average method to avoid initial transient data.

The instantaneous and mean volumetric efficiency of an axial piston pump can be plotted using MulticsPlotter. Volumetric efficiencies can be visualized as shown below:

Total Efficiency Calculation

The total efficiency of a pump is a measure of how effectively a pump converts input power into useful hydraulic power. It accounts for both the volumetric and hydromechanical efficiency. It can be defined as the ratio between effective output power and input power.

\[\eta_{t,P} = \frac{P_{P,e}}{P_{P,i}}\]

where, \(P_{P,e}\) represents effective output power and \(P_{P,i}\) represents input power.

The total efficiency of a hydraulic motor is a measure of how effectively the motor converts hydraulic power into useful mechanical output power. It accounts for both the volumetric and hydromechanical efficiency.

\[\eta_{t,M} = \frac{P_{M,e}}{P_{M,i}}\]

where, :math:P_{M,e} represents the effective output power and :math:P_{M,i} represents the input power.

Total efficiency accounts for both the volumetric and hydromechanical efficiency (discussed later). A sample calculation for a positive displacement machine is demonstrated below using a case of an axial piston pump.

\(P_{P,e}\) can be calculated as

\[P_{P,e} = Q_2 \cdot (P_2 - P_1)\]

Where, \(Q_{2}\) denotes the output flow and \(P_{2}\) and \(P_{1}\) denote the high and low pressure respectively.

\(P_{P,i}\) is equal to the torque (T) multiplied by shaft rotation speed (\(\omega\), rev/min).

Now torque can be calculated using the given formula:

\[T = \sum_{i}^{n=9} r _{pitch} \cdot \sin(\phi) \cdot F_z \cdot \tan(\beta)\]

Here, \(r_{pitch}\) represents the pitch radius of the piston, \(\phi\) represents the shaft rotation angle, \(F_z\) stands for the force along the shaft axis.

The mean total efficiency in Multics is calculated considering the moving average method to avoid initial transient data.

Hydromechanical Efficiency Calculation

Frictional losses resulting from moving parts and fluid shear increase the torque required to drive a pump operating at a given pressure compared to the ideal case. This aspect is quantified by the hydromechanical efficiency, also known as torque efficiency. The hydromechanical efficiency for a pump is defined as the ratio of the ideal shaft torque to the actual shaft torque.

\[\eta_{hm,P} = \frac{T_{P,i}}{T_{P,e}}\]

where, \(T_{P,i}\) represents the ideal shaft torque and \(T_{P,e}\) represents the actual shaft torque.

For a hydraulic motor, these losses result in a reduction of the output torque compared to the ideal case. The hydromechanical efficiency for a motor is the ratio of the actual output torque to the ideal output torque.

\[\eta_{hm,M} = \frac{T_{M,e}}{T_{M,i}}\]

where, \(T_{M,e}\) represents the actual output torque and \(T_{M,i}\) represents the ideal output torque.

We can also calculate the hydromechanical efficiency using the relation between three efficiencies as shown below:

\[\eta_t = \eta_v \times \eta_{hm}\]

Rearranging this equation to solve for the hydromechanical efficiency, we get:

\[\eta_{hm} = \frac{\eta_t}{\eta_v}\]

All the mean efficiencies for axial piston pump (lumped parameter model) can be plotted using MulticsPlotter, as shown in the figure.

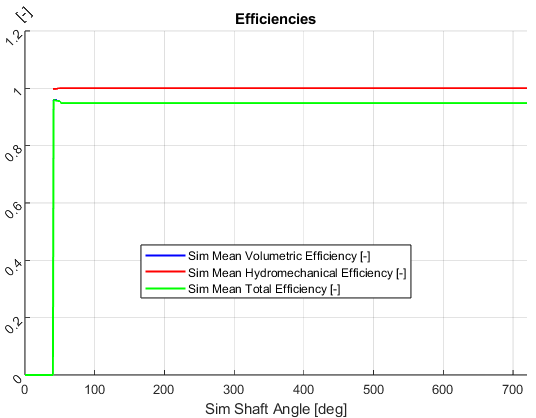
The above definition of efficiency is for an entire machine, meaning when ideally simulating all lubricating interfaces. However, Multics can simulate each individual component independently, and the volumetric and hydromechanical loss can depend on how many lubricating interfaces are included in the simulation. The main sources are cylinder block - valve plate interface, piston - cylinder interface, and slipper - swashplate interface. The leakage from those lubricating interfaces to the case chamber can contribute volumetric loss. Also, viscous and asperity contact dissipation can contribute hydromechanical loss. Thus, when simulating different lubrication interfaces or chambers, the efficiency results can be different.